amazonで「買っておいたことにする」みたいな機能が欲しいなとか思ったり。普通に購入して支払いもカードなりポイントなりで決済するんだけど、1ヶ月くらいamazon倉庫に置いておく。「近い内に(遅くとも2,3週間程度で)また買い物するはずだからそのときにまとめて送って」的な。あとでまとめて注文すればいいだろ、という話ではあるんだけど。
夜中に裏山を歩いていたらフクロウに遭遇した。全くの無音で飛んでくるので結構不思議。飛び立ったあとに枝のひずみエネルギーが開放されてカラカラ鳴る程度。よくよく耳を澄ますと少しだけ羽音が聞こえるかな、くらい。生き物らしい音が全くしない。そりゃ不吉の象徴とか言われるわけだ、みたいな納得がある。
***
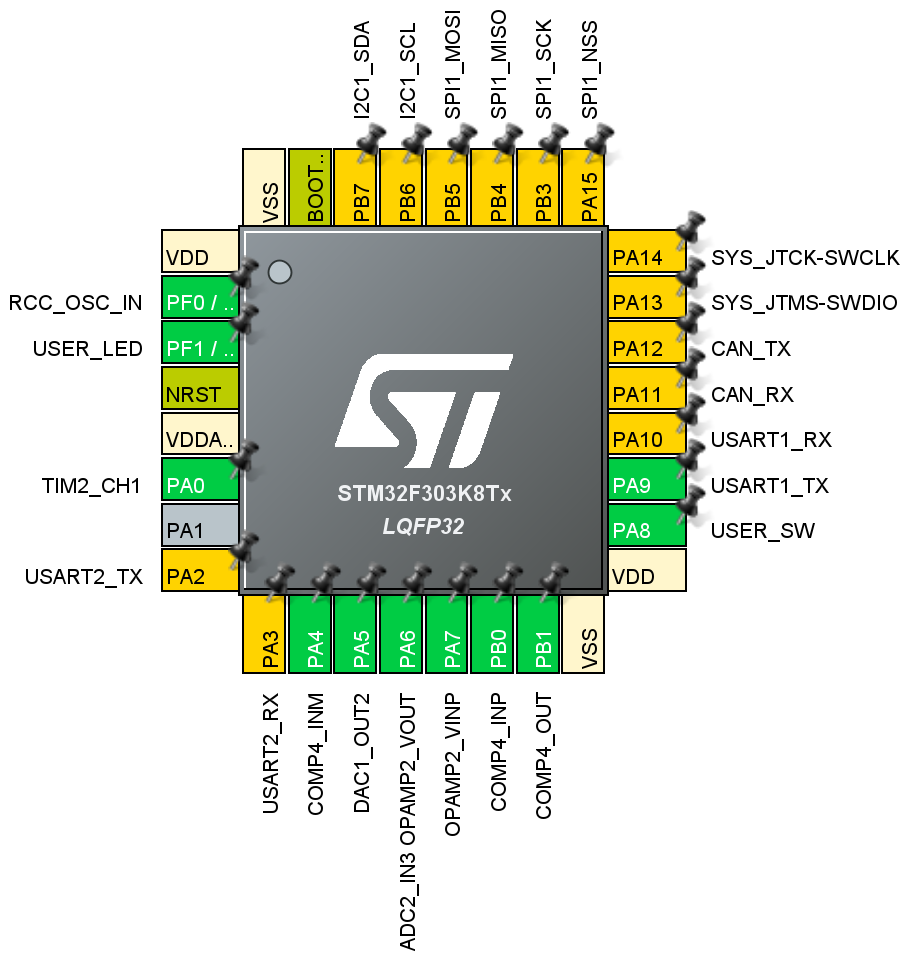
STM32G031J6Mで1-Wireデバイスの制御。一時期秋月で売っていたチップ。
今回はTIMで作ってみた。ch3でPWMを出して送信、受信時はch4でパルス幅を計測する。あんまりスッキリしないけど、一応1-wireに必要な機能はストロングプルアップも含めて実装。ストロングプルアップはEXTIとか割り込みが必要かと思ってたけど、結果的には非常に簡単に処理できた。
今回はRTOSは乗っていないのでポーリングで処理している。DMAを使えば1バイト分の転送とかをまとめてハードウェアで処理できるだろうけど、DMAで処理するのは結構面倒な気がする。特に送信用のARRとCCR3はメモリtoペリフェラル、受信用のCCR4はペリフェラルtoメモリだから、少なくとも2本のDMAが必要になる。タイマとかDMAの同期とかも考えるとなかなか大変そうだ。
STM32はGPIOをオープンドレインとプッシュプルで使えるので、オープンドレインで使えば外付けのダイオードが不要になる。また、プッシュプルに設定すればストロングプルアップとしても使える。ということで、最終ビットの立ち上がりエッジでGPIOをODからPPに切り替えれば、ストロングプルアップとして使える。ただ、ストロングプルアップ直前の1バイトはファンクションコマンドでマスターから送るだけだから、ODである必要はない。ということで、最終1バイトを送る前にPPへ変更している。1-WireにI2Cのクロックストレッチみたいな機能があるとちょっと困ったことになる。まあ、そういう機能はないはずなので、PPで送信しても問題ないはず。
タイマはch3が出力、ch4が入力で、どちらも同じピンに割り当てている。ただ、STM32CubeMXでは一つのピンにタイマの出力と入力を同時に割り当てることはできないから、この部分はユーザーコードで初期化している。
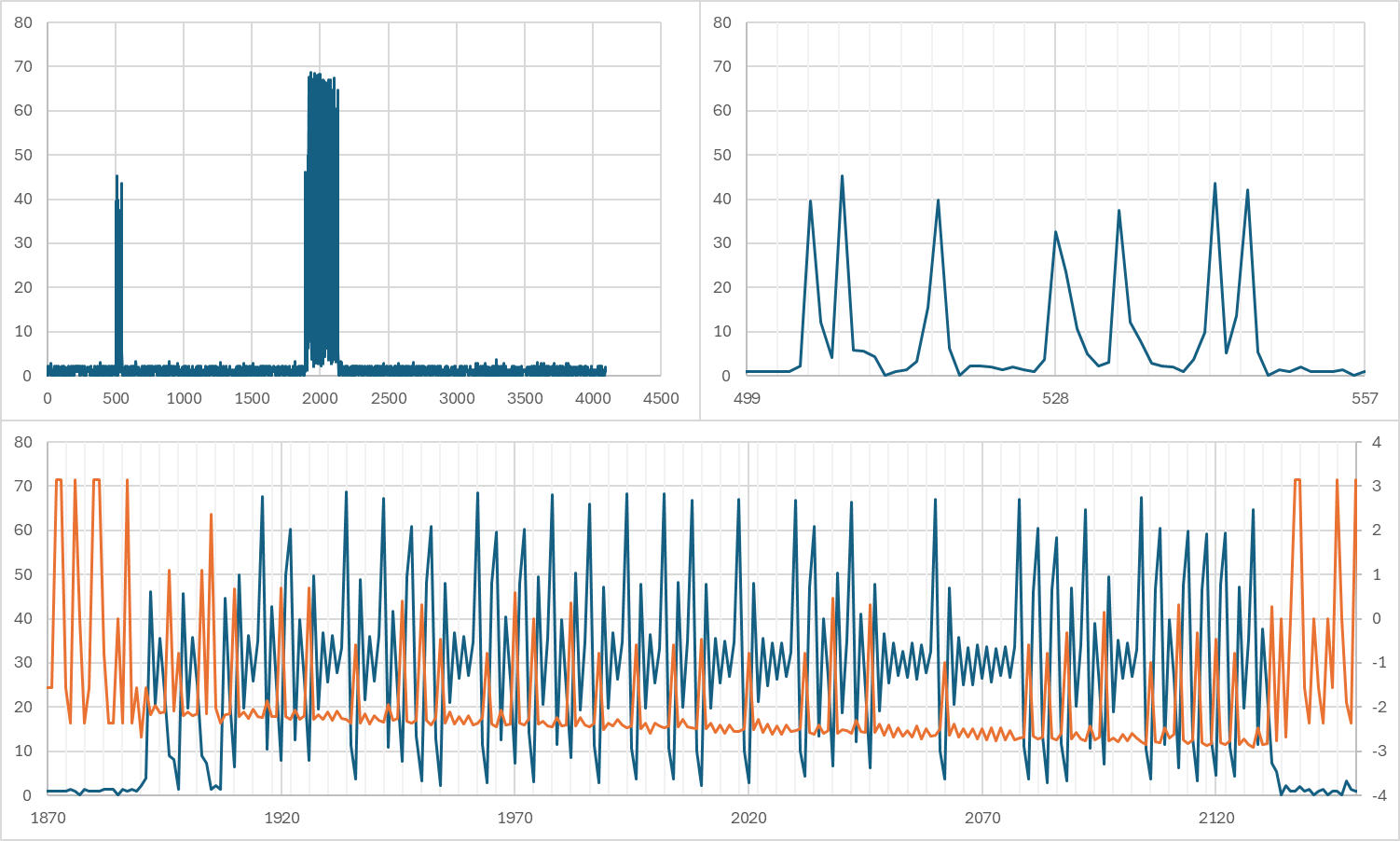
窓の外に置いたプローブで計測
1dC/div、1hour/div、左端が22時過ぎあたり。夜中なので直線状に温度が下降している。開始後2時間目あたりから1時間ほど温度が上がっているけど、ここは窓を開けていた時間。少し隙間を開けていた程度だけど、かなり影響するな。5時頃から温度降下が止まっているが、太陽が出てきたからかな。9時頃から急激に温度が上昇しているけど、天気が変わったりとかかな? 温度センサだけ見ても面白いけど、他のセンサも欲しくなるな。
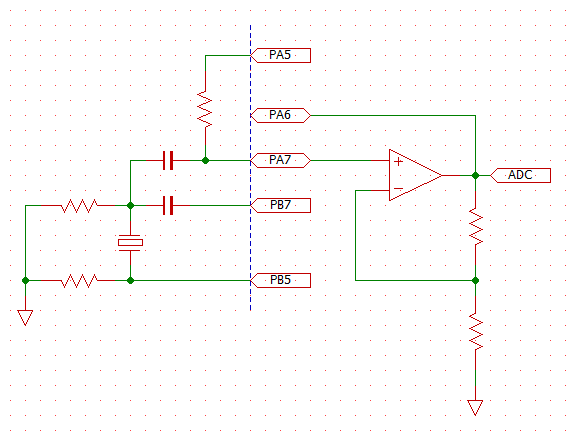
ハードウェアはこんな感じ
SOP8変換基板にSTM32を実装して、裏面に8x8のユニバーサル基板を貼り付けて、そこにSOT-89のレギュレータを乗せている。FT232系チップでUSBから5Vを取って、マイコンからはUARTの送信だけ。SOP側から出てる2本の端子はプログラムの書き込み用のSWD端子。
1-Wireデバイス側は一応3線式(GND, DQ, VDD)の接続にも対応しているけど、今回は2線式(GND, DQ)のセンサを接続している。というか、3線式ならFT232に直結できるので、わざわざマイコンを挟んで温度を測る必要もないしな。。。
小さいパッケージのSTM32
ブレッドボードに乗せるならこのあたりが楽で良い。QFP48だと変換基板が2列の四角形になるのでブレッドボードに載せられない。まあ、基板作れって話なんだけど。。。
***
気まぐれに、ワンセグチューナーで1090MHzを2Mspsで受信。
なんかそれっぽい信号が見えるな。
1000あたりは1.45us周期で15個のパルス位置があるので、Mode 3/A/Cの信号っぽい。Mode 3/A/Cはコードや高度が送られてくるけど、どっちが出てくるかは下から見てるとわからないのがな。
3000あたりのやつはMode Sだと思うけど、波形が変な形。おそらくクロックエラーでパルスを分離できていないだけだと思うんだけど。位相を見てみると、63kHz(58ppm)くらいの角速度。RTL-SDR blog v3ドングルがそこまでずれることはないだろうから、大部分は送信側のクロックエラーのはず。
Mode Sってどの程度の周波数エラーが許容されてるんだろうか? 2Mspsみたいなことをやらない限りはクロックエラーはある程度広く許容できそうな気がするし、飛行機みたいに温度環境が厳しい場所でこれだけ大量に普及させてるんだからある程度広く設定してあるはず。そうするとワンセグチューナーベースのADS-Bのデコーダがどうやって処理しているのかが謎いけど。
古い資料だと、モードSの周波数の許容偏差は15000ft以下のみを飛行するなら±3MHz、これを超える場合は±1MHz、ということらしい。最近だと±1MHzに統一かな? 専有帯域幅が10MHzを超えるようなシステムなので、許容偏差もそれに応じて広め。そもそも帯域幅2MHzとかの受信機で受信する信号じゃないからな。。。
別のサンプル
位相の回転はほとんど無い。しかし相変わらずパルス位置の復調がうまくいかない。
更に別のサンプル。rtl_tcp.exeが3.2Mspsくらいまで取れることがわかったので、試しに3.0Mspsでサンプリングしてみた(3.2Mspsだと2.048Mspsとかに比べて感度が低い気がする。デシメーションで処理利得が稼げないからかな。いちおう、rtl_tcp.exeではエラーログは出ず、FMラジオを復調すれば途切れずに聞こえるから、3.2Mspsが通っているはず)。
さっきよりはマシ。ちゃんとパルス間が0付近まで落ちてるし、プリアンブルの形も綺麗に見えてる。
試しにいくつかのサンプルを機械的にデコードしてみると、1個だけCRCが0になる(誤りが無いと考えられる)パケットが見つかった。DF17, CA5で、ICAOコードをFr24で検索するとちゃんと家の近くを飛んだログがある。ということで、正常にデコードできていると考えられる。
ただ、大半のパケットはCRCが0にならない。ビット位置がずれると正常に復号できないので、0.3bit幅ずつ数ビット分の幅をずらして総当たりでデコードしても、復調率は改善しない。開始位置のオフセットとクロックのオフセットで2次元のfor回してスキャンしたりすればあるいは……
短いパルスは3/A/Cの応答として復調すると、Fr24に記録されているSquawkと同じ値が時々出てくる。値は4箇所くらいに固まっているかな。普通民間の飛行機1機からはA/Cの2つの値が出てくるから、4個のグループがあるということは2機が飛んでいたということになる。ただ、Fr24のログだと航空機は1機しか記録されていない。もっとも、家のエリアはMLATは非対応だろうし、A/Cしか出していない機体(ADS-B out非対応機)が飛んでいた可能性は捨てきれない。
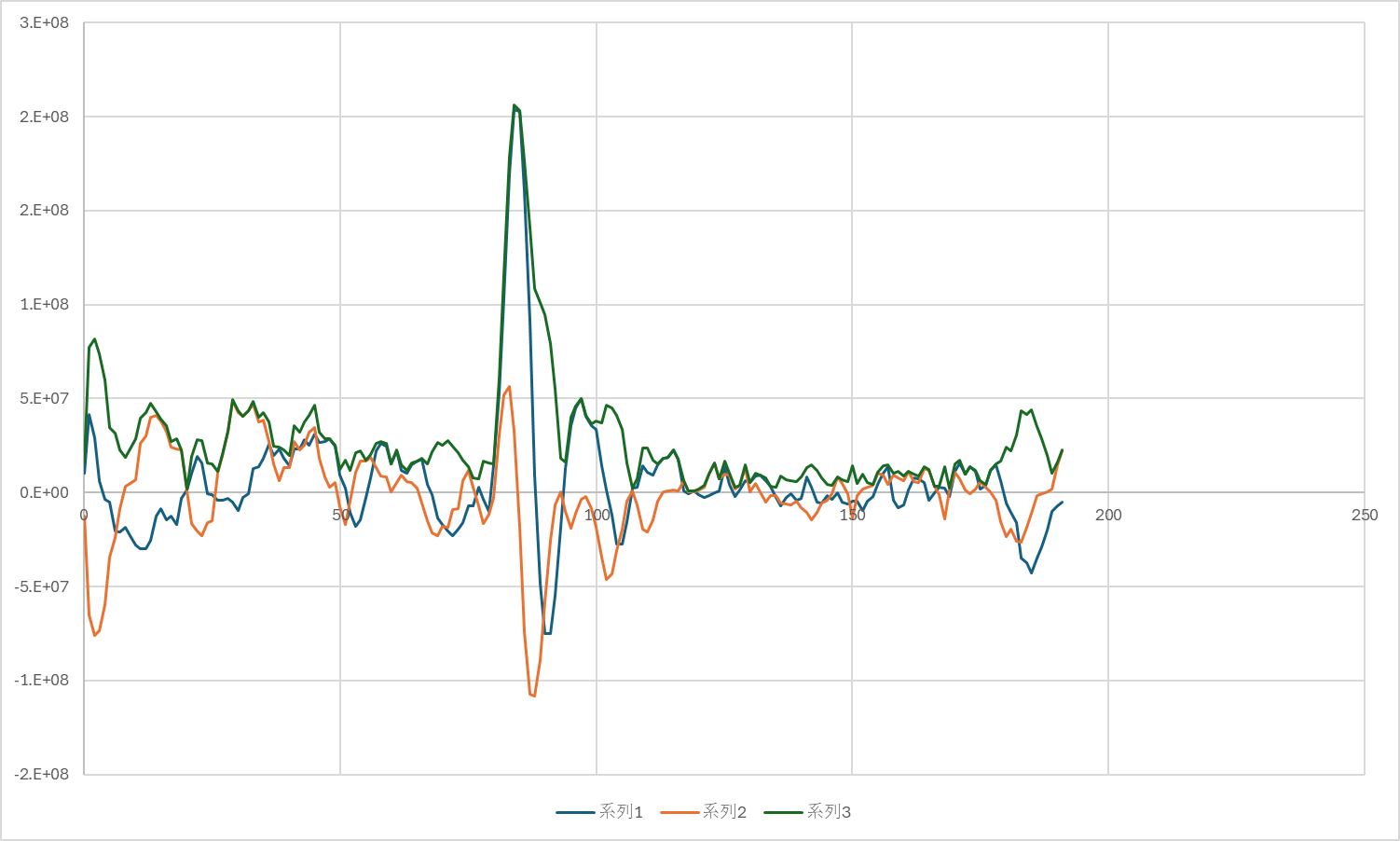
1機(特定のICAOアドレス)から送られてきたMode Sスキッターの位相をグラフ化してみると、傾向として位相回転は見えるけど、一貫性はあまりなさそうな感じ。送信機は今の時代にわざわざインコヒーレントに作る意味もないだろうし、水晶を逓倍して1090MHzを作ってゲートを通してからHPAに通して送信、みたいな回路だろうから、ある程度の安定性はあるはずなのだが。もう少し高いサンプリングレートで見れば安定して見えたりするんだろうか?
位相回転は送受信間の周波数オフセット(DC成分)に距離変化分のドップラー成分が乗っているはずだから、パルスの位相変化を見れば最接近の検出ができないかな、とか思ったんだけど。
うちのあたりは飛行場からも遠いし、その飛行場も便数がさほど多くないので、ATC SSRを受信するにはあまり条件が良くない。サンプルデータを集めるのも一苦労。
手軽にADS-Bを受信して遊ぶなら、ワンセグチューナーを3Mspsで走らせれば良さそう。もうちょっと簡単にデコードしたいなら4Mspsくらいあると安心だけど、とはいえそうするとAirspy miniあたりが必要になるので、ワンセグチューナー系の5,6倍くらいの値段になる。まあ、1回買えばしばらくは遊べるから思い切って買うという手もあるんだけど。ただ、おそらくAirspy系のドングルはlibrtlsdr(rtl_tcp.exeとか)からは触れないので、他の方法を考える必要がある。SpyServerでネットワークに接続できるけど、これは独自のプロトコルで、データを圧縮していたりするらしいから、触るのが面倒くさそう。SpyServerのOSSクライアントもあるらしいから、それを参考にクライアントを作るという手もあるけど。SpyServerはRTLドングルにも対応しているらしいから、とりあえず手持ちのドングルでSpyServerを起動して使えるかどうか確認して、使えそうならAirspy miniを買う、みたいな手もあるか。
ADS-Bは世界各地で受信できるデジタル変調だけど、デジタル復調の遊びとして使うにはあまり向いてないかな。そもそも変調方式の情報もほとんど見当たらないし、ちゃんとした資料が必要ならICAOから買わないとだめだろうし、個人で買えるようなものでもないだろうし。デジタル復調で遊ぶならワンセグとかを復調したほうが楽しい。いちおうワンセグとかフルセグは英語版のドキュメントが配布されているし。フルセグの方は基本的に暗号化データだから、復調後にエラー率を見たりして動作確認は行えるけど、復調したデータを見れないのが残念なところ。ADS-Bは一応は意味のあるデータが出てくるからな。ADS-Bはシングルキャリアのマンチェスタ符号、ISDB-TはOFDMで処理内容も全く違うから、そもそも比較対象でも無いんだけど。
*
軍用機(戦闘機とか)によく積んであるA/A TACANって飛行機間の距離を測定する機能だけど、Mode 3 XPDRでも距離は測れるわけで、軍用機で測距にMode 3を使わない理由ってなんだろう? TACANはチャンネルを設定できるけど、Mode 3だってコードを設定できるわけだから、周波数分割を使うか符号分割を使うかの違いでしかない。Mode 3だとATCに見えちゃうから、みたいな理由なのかな。そもそも軍用機には元からナビゲーション用にTACANインテロゲータが積んであるんだから、Mode 3を使うかTACANを使うかはどちらでも良くて、自由度が高いTACANを使った、みたいなことなんだろうか。